| x |
|---|
| 21.0 |
| 21.0 |
| 22.8 |
| 21.4 |
| 18.7 |
| 18.1 |
| 14.3 |
| 24.4 |
| 22.8 |
| 19.2 |
| 17.8 |
| 16.4 |
| 17.3 |
| 15.2 |
| 10.4 |
| 10.4 |
| 14.7 |
| 32.4 |
| 30.4 |
| 33.9 |
| 21.5 |
| 15.5 |
| 15.2 |
| 13.3 |
| 19.2 |
| 27.3 |
| 26.0 |
| 30.4 |
| 15.8 |
| 19.7 |
| 15.0 |
| 21.4 |
6. Indicateurs de Tendance Centrale
Les deux principaux indicateurs de tendance centrale sont la moyenne et la médiane, mais on trouve parfois aussi la valeur centrale (moyenne des valeurs minimale et maximale) ou le mode. Un indicateur de tendance centrale est toujours compris entre les valeurs maximale et minimale.
Moyenne
Moyenne Arithmétique
La moyenne arithmétique, souvent notée \(\bar{x}\), est l’indicateur de tendance centrale le plus connu. Elle est définie, en général, comme la somme des valeurs des observations divisée par le nombre total d’observations.
\[ \bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n} = \frac{1}{n} \sum_{i=n}^{n} x_i \]
Exemple
❔ Calculer la moyenne arithmétique, au centième prés.
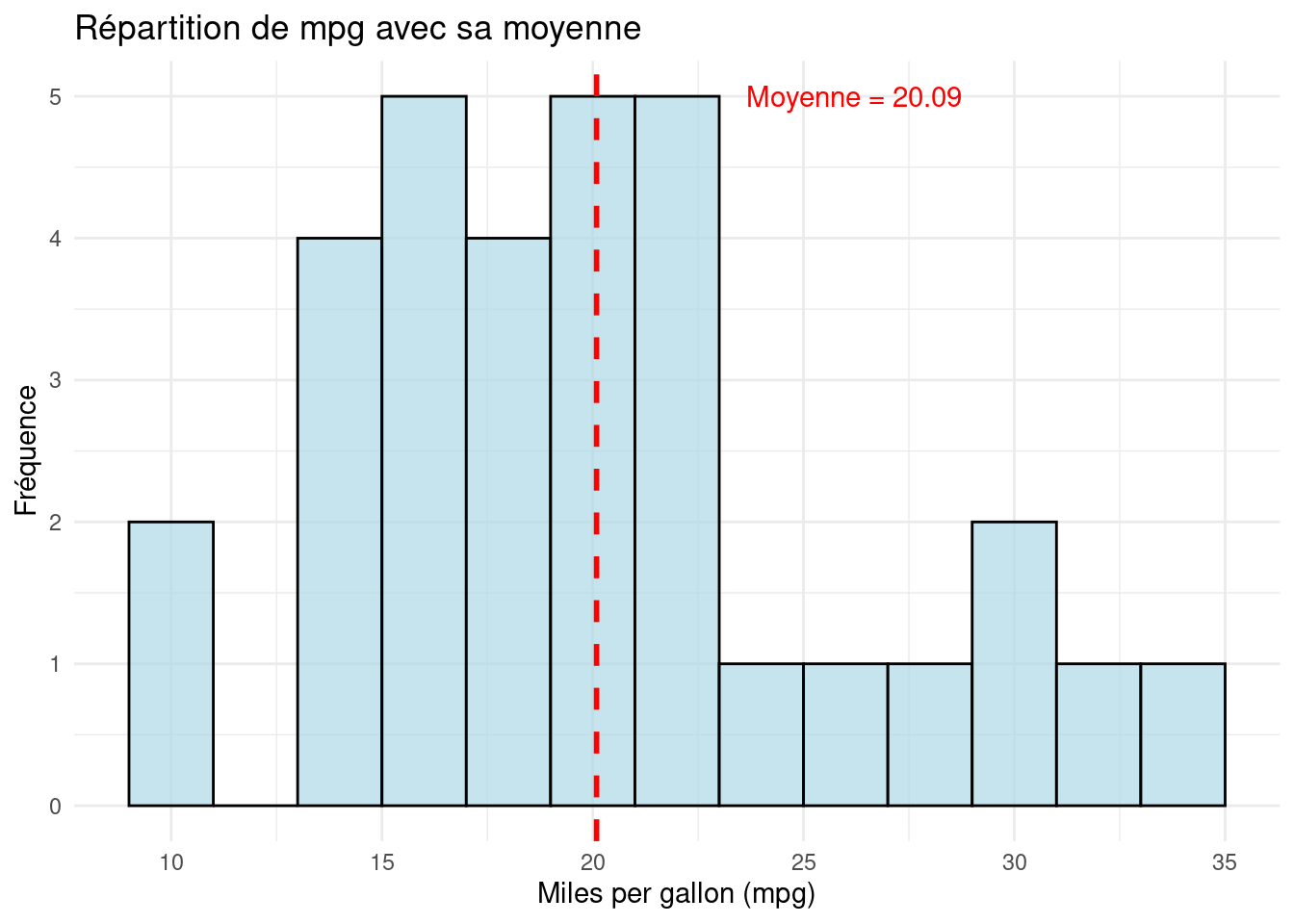
[1] 20.09Représentation graphique
Variable discrète
Pour une variable discrète dont les modalités \(m_i\) sont des valeurs exactes représentées en tableau:
\[ \bar{x} = \frac{\sum_{i=1}^{k} n_i \times m_i}{n} = \frac{n_1 \times m_1 + n_2 \times m_2 + \dots + n_k \times m_k}{n} \]
Où \(n_i\) est l’effectif associé à \(m_i\). Dans ce cas, \(\bar{x}\) est appelée la moyenne pondérée des données.
Exemple
| Nombre de vitesses | Effectif |
|---|---|
| 3 | 15 |
| 4 | 12 |
| 5 | 5 |
❔ Calculer la moyenne pondérée, au centième prés.
[1] 3.69Représentation graphique
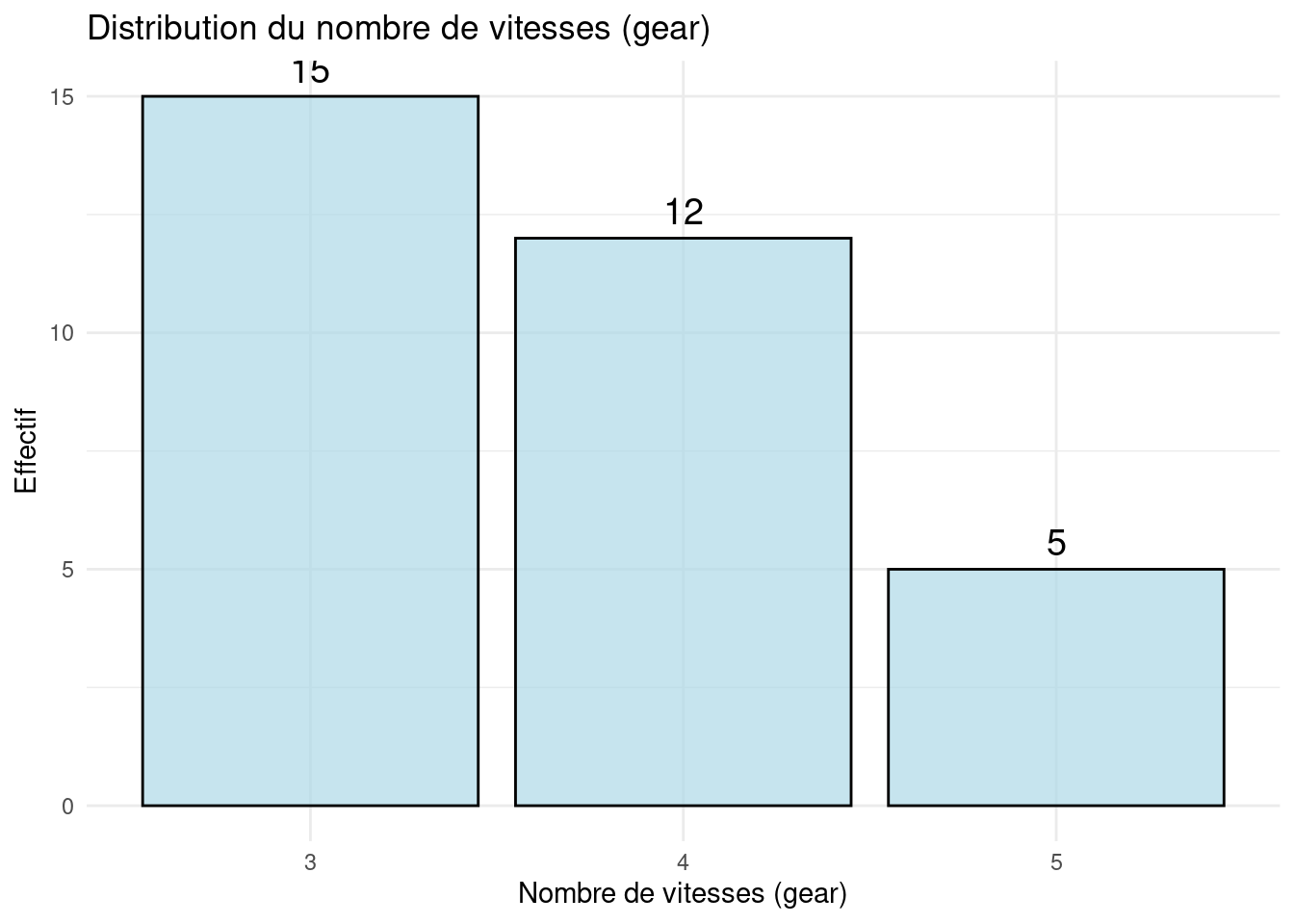
Variable continue
Pour une variable continue dont les modalités sont des classes représentées en tableau:
\[ \bar{x} = \frac{\sum_{i=1}^{k} n_i \times c_i}{n} = \frac{n_1 \times c_1 + n_2 \times c_2 + \dots + n_k \times c_k}{n} \]
Où \(c_i\) est le centre (milieu) de la \(i^e\) classe et \(n_i\) est son effectif associé. Dans ce cas, ${x} est également appelée la moyenne pondérée des données.
Exemple
| Intervalle de poids (wt) | Effectif |
|---|---|
| [1.51,2] | 4 |
| (2,2.49] | 4 |
| (2.49,2.98] | 4 |
| (2.98,3.47] | 9 |
| (3.47,3.96] | 7 |
| (3.96,4.45] | 1 |
| (4.94,5.43] | 3 |
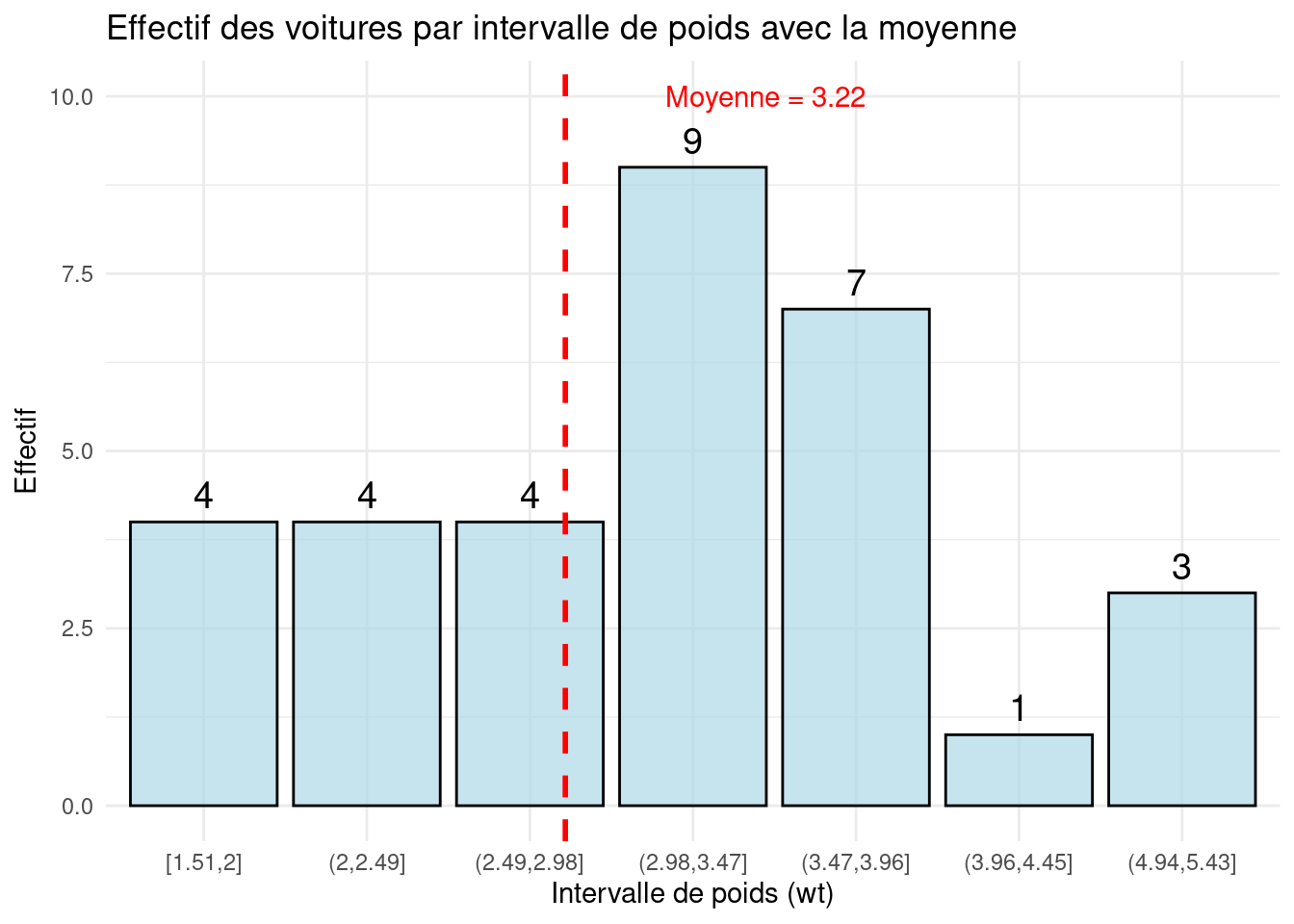
Calculer la moyenne pondérée, au centième prés
[1] 3.22Représentation graphique
Mode
Le mode est la valeur la plus fréquente du jeu de données.
C’est le seul indicateur de tendance centrale qui peut être utilisée sur des données nominales
Une répartition peut être unimodale ou plurimodale (bimodale, trimodale…), si deux ou plusieurs valeurs de la variable considérée émergent également, voire sans aucun mode (distribution uniforme) si toutes les valeurs de la variable considérée émergent également. Aussi, sa définition ne s’obtient pas directement comme une fonction des termes de la série.
Les variables qualitatives ou discrète
Le mode est la (ou les) modalité(s) da la varaible dont la valeur de l’effectif (ou fréquence) est la plus élevée.
Exemples
| x |
|---|
| 6 |
| 6 |
| 4 |
| 6 |
| 8 |
| 6 |
| 8 |
| 4 |
| 4 |
| 6 |
| 6 |
| 8 |
| 8 |
| 8 |
| 8 |
| 8 |
| 8 |
| 4 |
| 4 |
| 4 |
| 4 |
| 8 |
| 8 |
| 8 |
| 8 |
| 4 |
| 4 |
| 4 |
| 8 |
| 6 |
| 8 |
| 4 |
❔ Identifier le(s) mode(s) associés à ce jeu de donné
- 4
- 6
- 8
Représentation graphique
- Varibales discètes :
Warning: The dot-dot notation (`..count..`) was deprecated in ggplot2 3.4.0.
ℹ Please use `after_stat(count)` instead.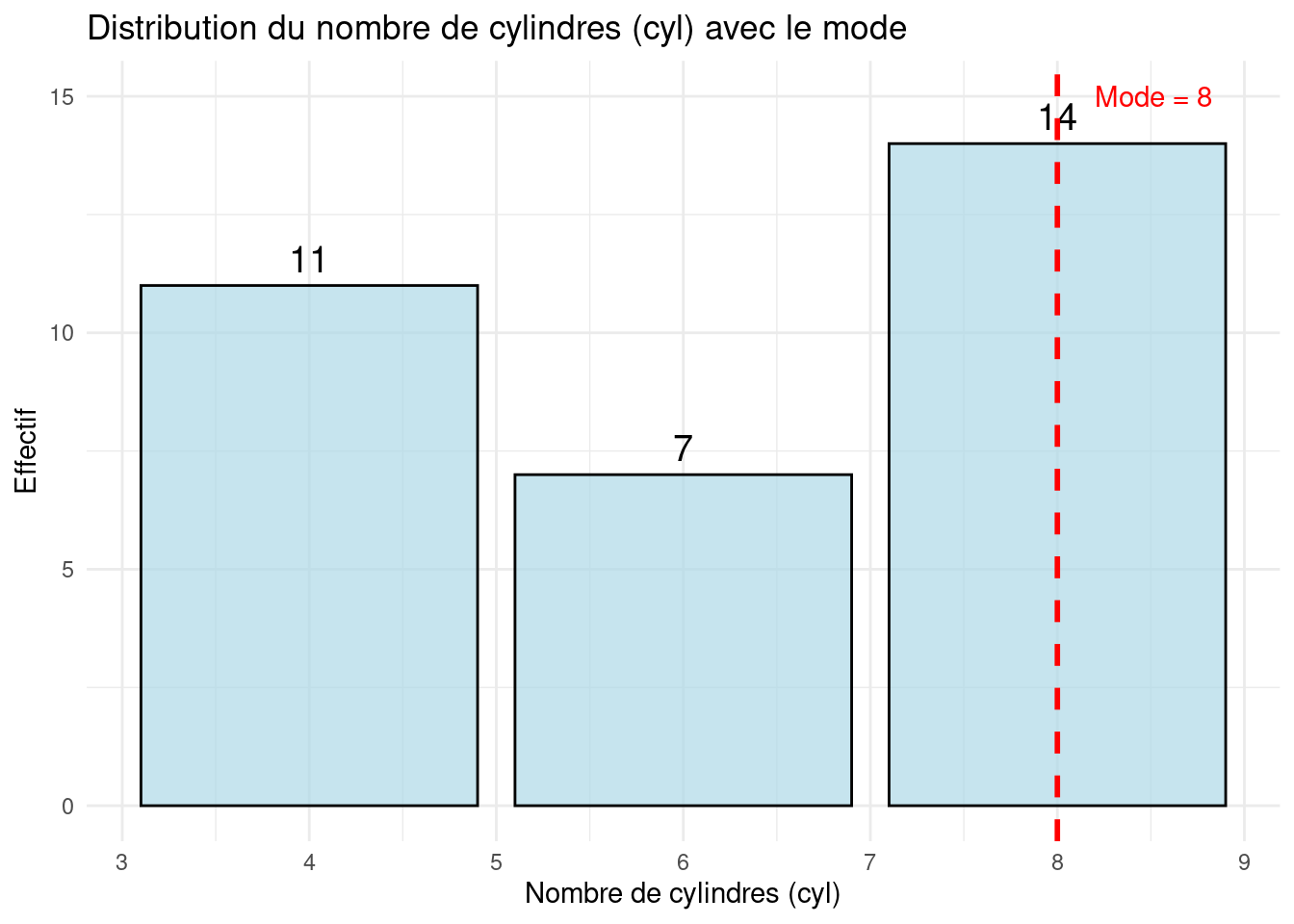
- Variables qualitatives
Warning: Use of `mtcars$am_label` is discouraged.
ℹ Use `am_label` instead.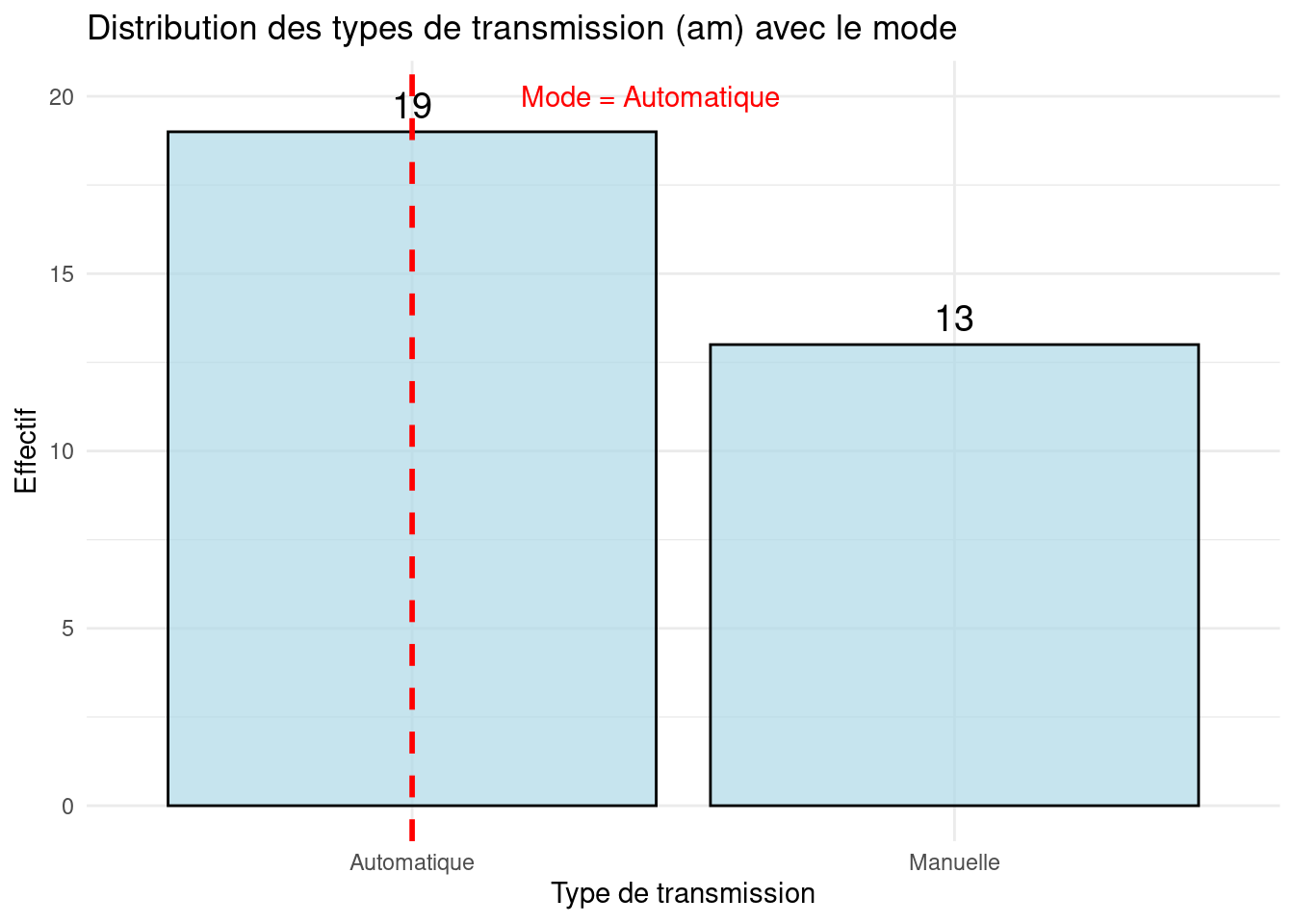
Les variables continues
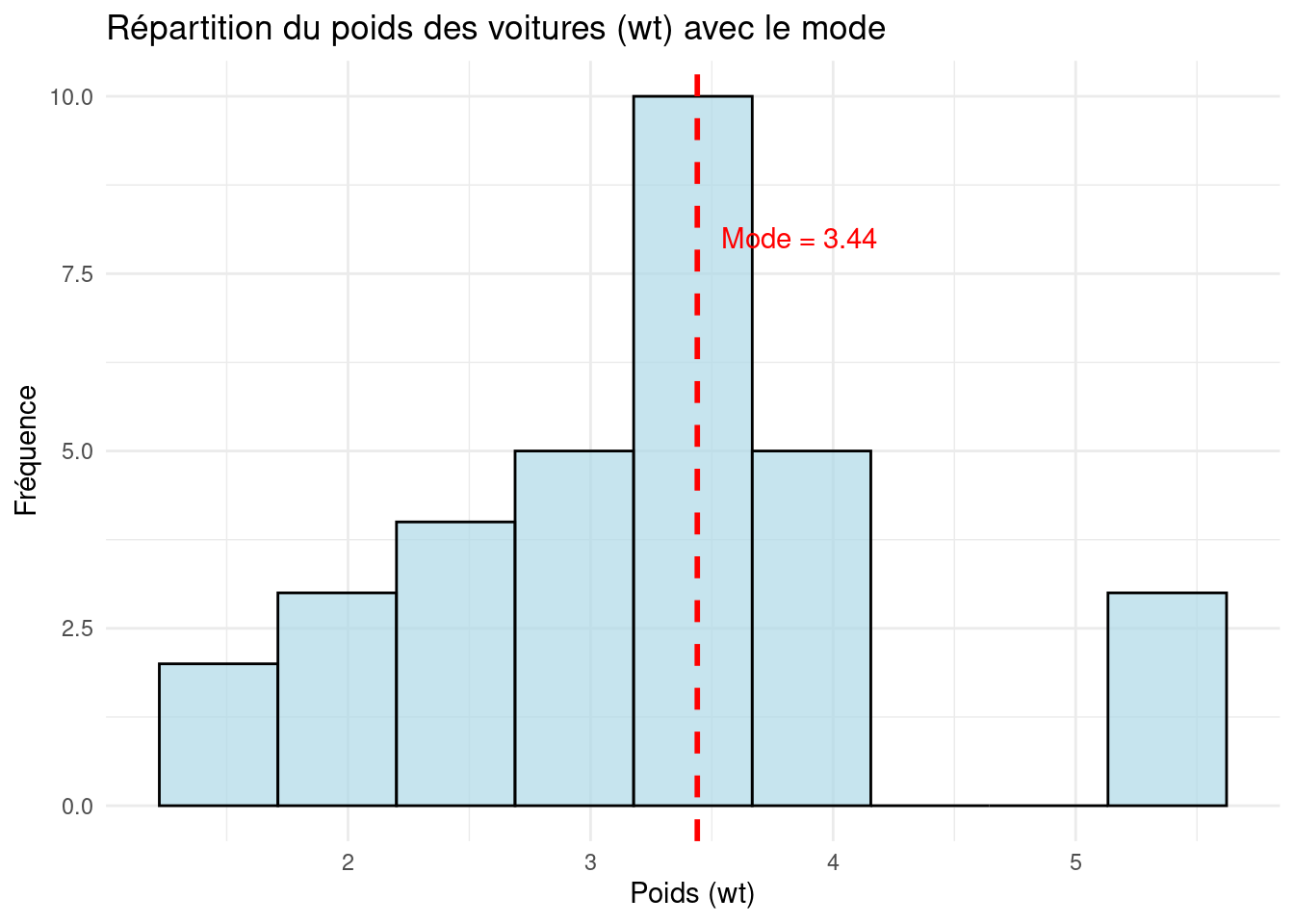
Dans le cas d’une répartition en classes d’amplitudes égales, la classe modale désigne celle qui a le plus fort effectif. La convention est d’appeler mode le centre de la classe modale. Si les classes sont d’amplitudes diverses, il convient de relativiser pour désigner ce paramètre. La classe modale est alors celle qui a la plus forte densité.
Le mode appartient à la classe modale (celle qui possède la plus grande hauteur). Soit \([a; b[\) la classe modale, le mode est calculé ainsi :
\[ Mode = a + \left((b - a) \times \frac{\Delta_1}{\Delta_1 + \Delta_2}\right) \]
Où:
- \(\Delta_1 = h_c - h_{c-1}\)
- \(\Delta_2 = h_c - h_{c+1}\)
Avec:
- \(h_c\) la hauteur de la classe modale \([a; b[\)
- \(h_{c-1}\) la hauteur qui précède \([a; b[\)
- et \(h_{c+1}\) la hauteur qui succède \([a; b[\)
Exemple
| Intervalle de poids (wt) | Effectif |
|---|---|
| [1.51,2] | 4 |
| (2,2.49] | 4 |
| (2.49,2.98] | 4 |
| (2.98,3.47] | 9 |
| (3.47,3.96] | 7 |
| (3.96,4.45] | 1 |
| (4.94,5.43] | 3 |
Identifier le mode
Représentation graphique